NAMA : Niko Aditya Kriswan
NIM : 21090114140154
Estimasi Parameter
Estimasi Parameter
-
Distribusi probabilitas memiliki
sejumlah parameter.
-
Nilai parameter-parameter tersebut
umumnya tidak diketahui.
-
Nilai parameter tersebut diperkirakan
berdasarkan nilai yang diperoleh dari pengolahan data.
-
Estimasi :
o
Estimasi
Tunggal (Point Estimates)
o
Rentang
Keyakinan (Coinfidence Intervals)
Estimasi
Tunggal (Point Estimates)
-
Nilai rata-rata sampel sebagai estimasi
nilai rata-rata populasi
-
Nilai simpangan baku sampel sebagai
estimasi nilai simpangan baku populasi :
Estimasi
Parameter θ
Dicari suatu rentang [L,U]
yang memiliki probabilitas (1 – α) bahwa rentang tsb mengandung θ.
-
L = batas bawah
rentang keyakinan
-
U = batas atas rentang keyakinan
-
(1
– α) = tingkat keyakinan (confidence level, confidence coefficient)
-
L dan U = variabel random
Contoh
Data pengukuran temperatur udara di Yogyakarta pada periode 1991
s.d. 2014 menunjukkan bahwa temperatur udara rata-rata di Yogyakarta adalah
30°C. Kita dapat memperkirakan bahwa temperatur udara rata-rata di Yogyakarta
adalah 30°C. Kita menyadari bahwa perkiraan tsb dapat salah; bahkan dari sisi
pengertian probabilitas, kita tahu bahwa temperatur udara rata-rata sama dengan
30°C adalah hampir tidak mungkin terjadi:
Batas Atas dan Batas Bawah
-
Metode Ostle: method of pivotal quantities
Dicari variabel random V yang merupakan fungsi parameter θ
(θ = unknown), tetapi distribusi V ini tidak bergantung pada
parameter yang tidak diketahui. Ditentukan v1 dan v2 sedemikian
hingga:
§ Persamaan
di atas diubah kedalam bentuk
prob(L < θ < U) = 1− α
§ L dan U
adalah variabel random dan fungsi V, tetapi bukan fungsi θ
Rentang Keyakinan μsuatu
distribusi normal
-
Mencari
interval [L,U] yang mengandung μ,
prob(L
< μ < U) = 1 – α
-
Misal
variabel random V:
o
V berdistribusi t
dengan (n – 1) degrees of freedom
o
n adalah jumlah sampel
yang dipakai untuk menghitung nilai rata-rata sampel
Contoh
:


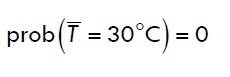





Tidak ada komentar:
Posting Komentar